HOME LAB OPJzM

FLUKA:	START	Primary	Geometry	Media	Estymatory	Problemy
ROOT	Projekt VELO	Projekt “Zasięg”	Projekt “Źródła”	Wyniki studentów

Kategoria GEOMETRY

Rozpoczynamy budowanie geometrii.
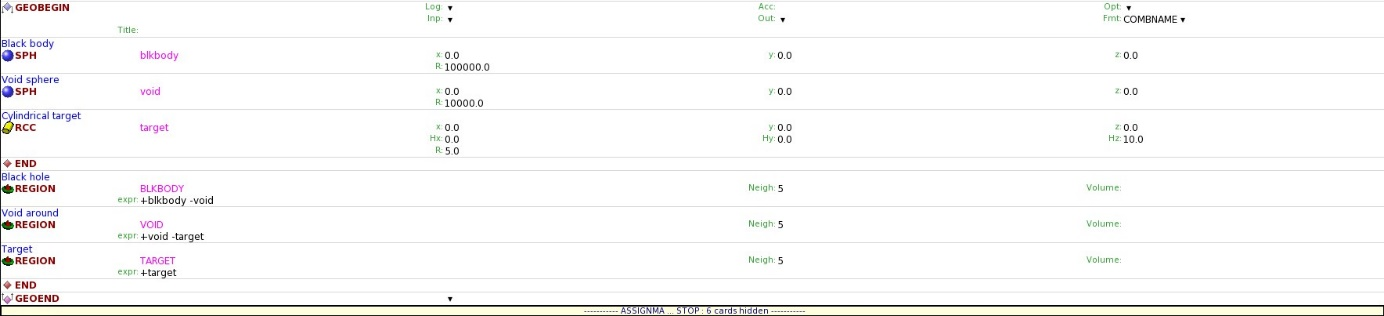
Karta GEOBEGIN pozostaje niezmieniona. Szablon domyślnie generuje geometrię składającą się z dwóch olbrzymich koncentrycznych sfer o nazwach blkbody i void (obowiązkowe – nie usuwać, można zmienić im kształt) oraz tarczy cylindrycznej o nazwie target. Możemy zamienić tarczę na tarczę o innym kształcie poleceniem: Card → Change → Geometry → Bodies → Wybór kształtu, lub dodać dodatkowy kształt geometryczny (dodać jego kartę) poleceniem: Card → Add → Geometry → Bodies → Wybór kształtu. Dodawanie komentarza do karty: Kliknąć prawym przyciskiem myszy → Insert comment

Przydatne kształty geometryczne:

kod	opis
RPP	Prostopadłościan o krawędziach równoległych do osi układu współrzędnych, wyznaczony przez współrzędne: Xmin, Xmax, Ymin, Ymax, Zmin, Zmax
BOX	Prostopadłościan o dowolnej orientacji w przestrzeni. Używanie kształtu BOX jest na ogół niezalecane. Można go zastąpić kombinacją płaszczyzn nieskończonych, PLA, XYP, XZP, YZP, które są łatwiejsze do zdefiniowania; x, y, z: współrzędne wierzchołka; H1x, H1y, H1z: współrzędne wektora odpowiadającego wysokości; H2x, H2y, H2z: współrzędne wektora odpowiadającego szerokości H3x, H3y, H3z: współrzędne wektora odpowiadającego długości. Wektory 1, 2 i 3 muszą być wzajemnie prostopadłe.
SPH	Sfera definiowana przez 4 liczby: x, y, z: współrzędne środka R: promień
RCC	Walec kołowy prosty, o dowolnej orientacji w przestrzeni, definiowany przez 7 liczb: x, y, z: współrzędne środka jednej z podstaw kołowych Hx, Hy, Hz: współrzędne wektora odpowiadającego wysokości walca skierowanego ku drugiej podstawie; R: promień walca
REC	Walec eliptyczny prosty, o dowolnej orientacji w przestrzeni, definiowany przez 12 liczb: x, y, z: współrzędne środka jednej z podstaw eliptycznych, Hx, Hy, Hz: współrzędne wektora odpowiadającego wysokości walca skierowanego ku drugiej podstawie; R1x, R1y, R1z: odpowiednie półosi małe podstawy eliptycznej walca, R1x, R1y, R1z: odpowiednie półosi wielkie podstawy eliptycznej walca

Ważne jest, by poszczególne kształty (BODIES) nie dotykały się (nie posiadały wspólnych płaszczyzn)! Definiowanie kształtów geometrycznych musi być zakończone kartą END.

Przystąpimy teraz do tworzenia obszarów (REGIONs) geometrii. W dalszych krokach będzie można przypisać każdemu obszarowi materiał, którym jest wypełniony.

Każdy obszar geometrii jest opisany jako kombinacja logiczna jednego lub więcej kształtów geometrycznych. Wykorzystuje się w tym celu trzy symbole operacji algebry boolowskiej:

symbol	opis
-	różnica
+	suma
OR	przecięcie (część wspólna)

Definiowanie obszarów geometrii musi być zakończone kartą END.

Następnym etapem jest wypełnienie utworzonych regionów materiałem. Pomaga w tym Kategoria MEDIA